What Graph Goes Up Down and Up Again
Degrees, Turnings, and "Bumps"
Graphs of polynomials don't always head in simply 1 direction, like nice nifty straight lines. Instead, they can (and usually practise) turn around and head dorsum the other way, peradventure multiple times. Each time the graph goes down and hooks back up, or goes up and and then hooks back down, this is a "turning" of the graph.
I refer to the "turnings" of a polynomial graph as its "bumps". This isn't standard terminology, and you'll learn the proper terms (such as "local maximum" and "global extrema") when y'all go to calculus, but, for now, we'll talk about graphs, their degrees, and their "bumps".
For example, the post-obit graph has three bumps, as indicated past the arrows:
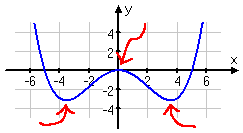
Content Continues Below
Beneath are graphs, grouped according to degree, showing the different sorts of "bump" collection each caste value, from two to six, can have. Compare the numbers of bumps in the graphs below to the degrees of their polynomials. In particular, note the maximum number of "bumps" for each graph, as compared to the degree of the polynomial:
caste 2:
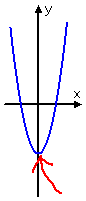
i crash-land
degree 3:
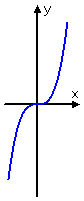
nix bumps, but one flex point
degree three:
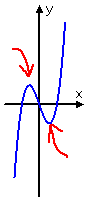
two bumps
degree four:
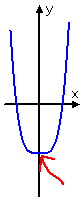
i (flattened) bump
degree 4:
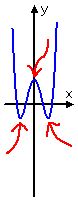
three bumps
caste five:

zero bumps, but one flex point
degree v:
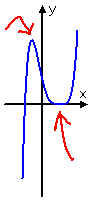
two bumps (ane flattened)
caste five:
four bumps
caste half dozen:
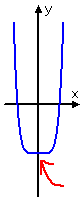
one (flat) bump
caste vi:
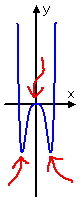
three bumps (i flat)
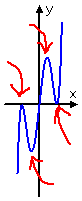
degree vi:
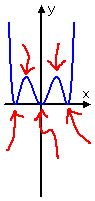
5 bumps
You can see from these graphs that, for degree northward , the graph will take, at almost, n − 1 bumps. The bumps represent the spots where the graph turns back on itself and heads back the way it came. This change of management ofttimes happens because of the polynomial's zeroes or factors. Just extra pairs of factors (from the Quadratic Formula) don't prove upwards in the graph as anything much more visible than just a piddling extra flexing or flattening in the graph.
Because pairs of factors have this habit of disappearing from the graph (or hiding in the flick as a little bit of actress flexture or flattening), the graph may have 2 fewer, or four fewer, or vi fewer, etc, bumps than you might otherwise expect, or it may take flex points instead of some of the bumps. That is, the caste of the polynomial gives you the upper limit (the ceiling) on the number of bumps possible for the graph (this upper limit being one less than the degree of the polynomial), and the number of bumps gives you the lower limit (the floor) on caste of the polynomial (this lower limit being one more than the number of bumps).
We can utilize this information to brand some intelligent guesses about polynomials from their graphs, and well-nigh graphs from their polynomials. For instance:
-
What is the minimum possible degree of the polynomial graphed below?
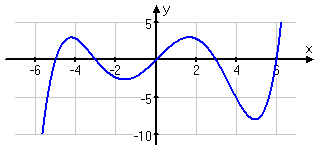
Given a polynomial's graph, I tin can count the bumps. The degree of the polynomial volition be no less than one more than than the number of bumps, merely the caste might be three more than that number of bumps, or 5 more than, or....
Since in that location are iv bumps on the graph, and since the end-beliefs confirms that this is an odd-degree polynomial, then the caste of the polynomial is 5, or maybe 7, or maybe 9, or... Simply this exercise is asking me for the minimum possible caste. And so my answer is:
The minimum possible degree is 5.
-
Given that a polynomial is of degree six, which of the following could be its graph?




To respond this question, I have to remember that the polynomial's degree gives me the ceiling on the number of bumps. In this case, the caste is 6, so the highest number of bumps the graph could have would be 6 − i = 5. But the graph, depending on the multiplicities of the zeroes, might take merely 3 bumps or perchance but one crash-land.
(I would add 1 or iii or 5, etc, if I were going from the number of displayed bumps on the graph to the possible degree of the polynomial, but here I'k going from the known degree of the polynomial to the possible graph, so I subtract. ). If you're not sure how to go along rail of the relationship, think about the simplest curvy line you've graphed, being the parabola. It has degree 2, and has 1 crash-land, being its vertex.)
Besides, I'll want to check the zeroes (and their multiplicities) to see if they requite me whatsoever boosted information. I'll consider each graph, in turn.

Graph A: This shows ane bump (so not also many), only only two zeroes, each looking similar a multiplicity-1 zero. This is probably merely a quadratic, only it might possibly be a sixth-degree polynomial (with iv of the zeroes beingness circuitous). I would have expected at least one of the zeroes to be repeated, thus showing flattening every bit the graph flexes through the axis. But this could maybe be a sixth-degree polynomial's graph.

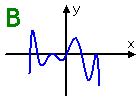
Graph B: This has seven bumps, and so this is a polynomial of degree at least eight, which is too high. This graph cannot perchance be of a degree-six polynomial.

Graph C: This has three bumps (so not too many), it'due south an even-caste polynomial (existence "upward" on both ends), and the naught in the middle is an even-multiplicity zero. Too, the bump in the middle looks flattened at the axis, so this is probably a repeated cypher of multiplicity iv or more. With the 2 other zeroes looking similar multiplicity-ane zeroes, this is very probable a graph of a 6th-degree polynomial.

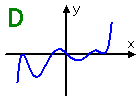
Graph D: This has six bumps, which is too many; this is from a polynomial of at least degree vii. On acme of that, this is an odd-degree graph, since the ends head off in opposite directions. So this can't peradventure be a sixth-degree polynomial.

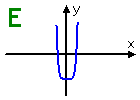
Graph E: From the end-beliefs, I can tell that this graph is from an fifty-fifty-caste polynomial. The i bump is fairly flat, then this is more than than merely a quadratic. This might be the graph of a sixth-degree polynomial.

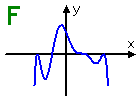
Graph F: This is an even-caste polynomial, and it has five bumps (and a flex point at that third zero). But looking at the zeroes, the left-almost zero is of even multiplicity; the next goose egg passes right through the horizontal axis, so it's probably of multiplicity 1; the next zero (to the right of the vertical axis) flexes as it passes through the horizontal axis, so it's of multiplicity 3 or more; and the zippo at the far right is some other even-multiplicity zero (of multiplicity two or four or...). Calculation these up, the number of zeroes is at least 2 + 1 + 3 + two = 8 zeroes, which is way too many for a degree-six polynomial. The bumps were right, but the zeroes were wrong. This tin can't peradventure be a caste-six graph.

Graph G: The graph's left-hand stop enters the graph from above, and the correct-hand stop leaves the graph going down. Since the ends head off in reverse directions, then this is another odd-degree graph. As such, it cannot possibly be the graph of an even-degree polynomial, of degree six or any other even number.

Graph H: From the ends, I tin see that this is an even-caste graph, and at that place aren't also many bumps, seeing as at that place'southward only the ane. Looking at the two zeroes, they both await like at least multiplicity-3 zeroes. So this could very well be a caste-six polynomial.
So I've determined that Graphs B, D, F, and G can't possibly exist graphs of degree-six polynomials. Graphs A and E might be degree-half-dozen, and Graphs C and H probably are. This question asks me to say which of the graphs could represent the graph of a polynomial role of degree six, so my respond is:
Graphs A, C, E, and H
To help you continue directly when to add together and when to subtract, remember your graphs of quadratics and cubics. Quadratics are caste-ii polynomials and have ane bump (always); cubics are degree-three polynomials and have two bumps or none (having a flex point instead). So going from your polynomial to your graph, you lot subtract, and going from your graph to your polynomial, y'all add. If you know your quadratics and cubics very well, and if yous remember that y'all're dealing with families of polynomials and their family characteristics, you shouldn't have any trouble with this sort of do.
Source: https://www.purplemath.com/modules/polyends4.htm
0 Response to "What Graph Goes Up Down and Up Again"
Post a Comment